Two Methods with the Riccati Equation to Seek Traveling Wave Solutions for the Simplified Modified Camassa-Holm Equation

Abstract

Background and Objectives : Nonlinear evolution equations (NLEEs) are crucial in modeling numerous physical phenomena, from plasma physics to fluid mechanics. The investigation of finding solutions to nonlinear evolution equations plays an important role since those solutions can explain a variety of the problems' natural events, such as solitons, vibrations, and finite-speed propagation. There are two fundamental kinds of solutions for NPDEs: exact solutions and analytical solutions. In this work, we solve the simplified modified Camassa-Holm (SMCH) equation in the following form:

                                               _t + 2k_x - _xxt + s²_x = 0,

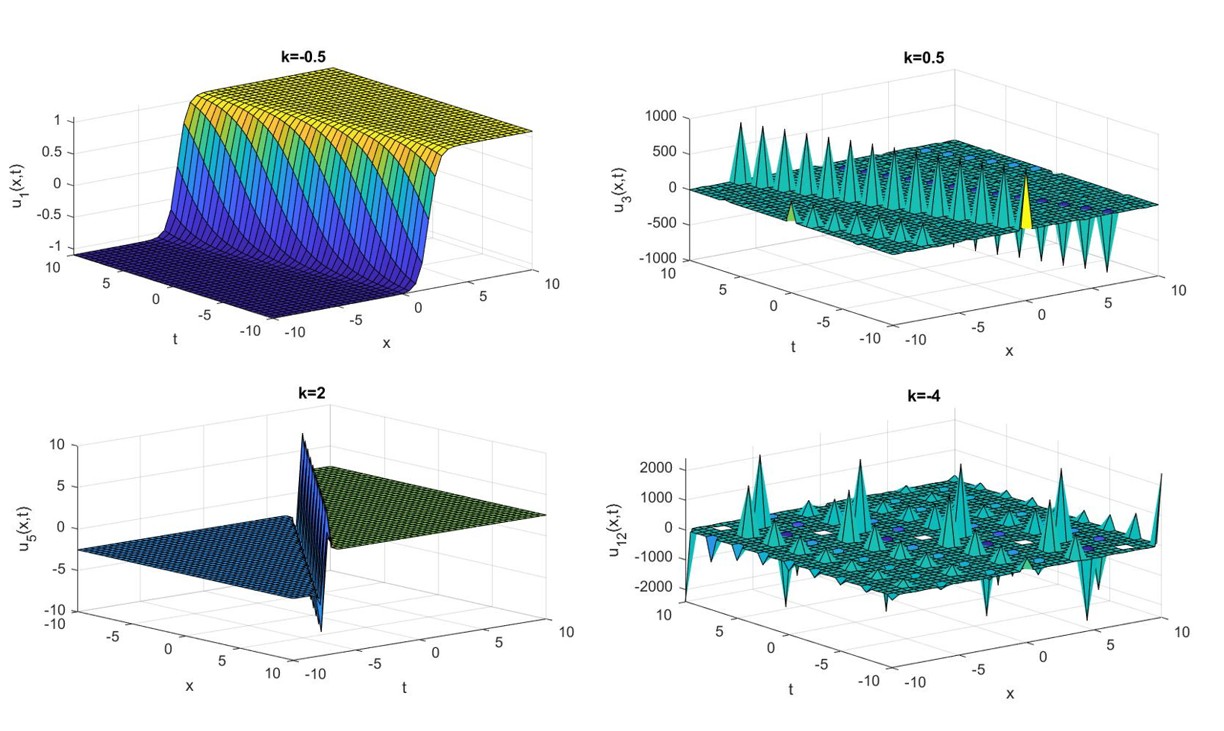
where s > 0, k  is a real constant, and (x,t) represents the fluid velocity in the x-direction. We employ the traveling wave transformation to transform the simplified modified Camassa-Holm (SMCH) equation, which is a nonlinear partial differential equation, into nonlinear ordinary differential equations. Then, we solve the equation using the simple equation method with the Riccati equation and the modified extended tanh function method. Two classes of exact explicit solutions, which are in the form of generalized hyperbolic functions and generalized trigonometric functions. Additionally, the results by the simple equation method with the Riccati equation and the modified extended tanh function method are vital tools for handling further models arising in applied science and new physics. For detailed physical dynamical representation, the results can be transformed into kink waves and periodic waves. Their graphical representations are 2-D and 3-D graphs.

Methodology : Using the simple equation method with the Riccati equation and the modified extended tanh function method to solve the simplified modified Camassa-Holm (SMCH) equation. There are four main steps involved in the simple equation method with the Riccati equation:

Step 1. Wave transformation: combining the independent variables x and  t  into one variable, = x - t.  Then (x,t)= () and = x-t, where is the speed of a traveling wave.

Step 2. Solution assumption: suppose that the solution is in the following form: () = a_iGⁱ() and  G¹() conform to the following Riccati equation, G¹() = G² () + , where the constants and are nonzero.

Step 3. Finding the integer M : the positive integer M  that occurs in the solution (step 2) can be estimated by taking into account the homogeneous balance between the highest-order derivative and the nonlinear terms appearing in the ordinary differential equation.

Step 4. Obtaining a solution: In order to determine , , and a_i , we must first find all terms whose coefficients are of the same order Gⁱ , i = 0, 1, 2, 3,...  and then set those terms to zero. We therefore have the exact traveling wave solution.

There are five main steps involved in the modified extended tanh function method, which are as follows:   

Step 1. Wave transformation: combining the independent variables x and  t into one variable, = x -  t. Then (x, t) = (), = x -  t.

Step 2. Solution assumption: suppose that the solution in the following for () = a₀ +      (a_iZⁱ () + b_iZ^-i () )   and  Z' (), conforms to the following Riccati equation,   Z' () = +  Z² (), in which  is a constant.

Step 3. Finding the integer M :  the positive integer  M  that occurs in the solution (step 2) can be estimated by taking into account the homogeneous balance between the highest-order derivative and the nonlinear terms appearing in the ordinary differential equation.

Step 4. Substitute the solution (step 2) and its derivative, as well as Z' ()= +  Z² (),    into the ordinary differential equation. Following that, by equating our Zⁱ , (i  =0, 12,...), coefficients to zero, we derive an algebraic system of equations that can be solved to determine the values of a_i , b_i , and .

Step 5. To find the exact traveling wave solutions, substitute the values of a_i , b_i , ,  and from the solutions of Z' ()= +  Z² (),   into  () = a₀ +      (a_iZⁱ () + b_iZ^-i () )     as follows.                                                 

Main Results: The exact traveling wave solutions of the simplified modified Camassa-Holm (SMCH) equation by using the simple equation method with the Riccati equation, in which solutions 1-2 are shown by hyperbolic functions and solutions 3-4 are shown by trigonometric functions, are as follows:

                    _1,2 (x,t) = tanh   ,

                    _3,4 (x,t) = tan ,

where  =   , >0, V  = 1.  And the exact traveling wave solutions of the simplified modified Camassa-Holm (SMCH) equation by using the modified extended tanh function method, in which solutions 5-8 are shown by hyperbolic functions and solutions 9-12 are shown by trigonometric functions, are as follows:

_5,6 (x,t) = ,

_7,8 (x,t) = ,

_9,10 (x,t) =  ,

_11,12 (x,t) = ,

where = ,

 

Conclusions : The exact traveling wave solutions of the simplified modified Camassa-Holm (SMCH) equation using the simple equation method with the Riccati equation and the modified extended tanh function method. The resulting solutions are represented by hyperbolic and trigonometric functions, which can be physically converted into kink and periodic waves. The findings further the solution form of hyperbolic functions, which can be transformed into kink waves, and the solution form of trigonometric functions, which can be transformed into periodic waves.  Moreover, both the simple equation method with the Riccati equation and the modified extended tanh function method rely on the Riccati equation and are straightforward to comprehend. Also, this study demonstrates that the suggested method is appropriate and very useful for determining precise solutions to the exact traveling wave solutions to the simplified modified Camassa-Holm (SMCH) problem. The method works reliably and effectively yields accurate solutions for solitary waves.