π-Phase State in a Superconductor-Ferromagnet Trilayer

Abstract

Background and Objectives : Oscillations of superconducting state properties in ferromagnetic layers are observed in hybrid layered systems composed of superconducting and ferromagnetic materials. The tunneling of electron Cooper pair wave functions from the superconducting region into the ferromagnetic region, governed by quantum mechanical principles, induces a superconducting state in non-superconducting materials. A deep understanding of the hybrid layered system phenomenon is crucial for fulfilling technological demands for next-generation electronic devices that operate through magnetic control. The phase shift of oscillating electron Cooper pair wave functions, completing one cycle of motion, results from the periodicity property defined as the sum of unit cell thicknesses of the layered system. Theoretically, when the electron Cooper pair wave function completes one cycle, there are only two possible values for the phase shift: zero and π. The π state of superconductivity is a state achievable in hybrid layered systems: superconducting-ferromagnetic-superconducting and multilayered systems where superconductors alternate with ferromagnets. The physics of the π state, viewed through the lens of quantum mechanical wave functions, differs from the zero-phase state due to even/odd spatial symmetry around the wave function's center point. Specifically, the π state corresponds to odd spatial symmetry of the wave function, while the zero-phase state represents even symmetry. Identifying the actual existence of the π state in layered systems is challenging due to the complexity of the physical data from synthesized composite materials and theoretical analysis methods. The following physical parameters characterize the layered system: normal state conductivity, diffusion coefficient, exchange energy of the ferromagnet and contact resistance at the interface between the superconducting and ferromagnetic layers.The difficulty in classifying the phase states stems from the last two parameters; these cannot be directly measured experimentally. Additionally, interfacial resistance is a parameter calculated from many-body quantum mechanics theory and cannot be fully measured but influences the oscillations of the superconducting state.Identifying the conditions controlling the emergence of the π state remains a subject of study in this article.This work confirms the possibility of the π state in superconducting-ferromagnetic-superconducting layered systems through numerical simulation results.

Methodology : In the limit where the diffusion length defined by the electron pair range is greater than the free path of electrons, The Usadel equations become suitable for analyzing the oscillations of the critical temperature in ferromagnetic layers within hybrid superconducting-ferromagnetic-superconducting layered systems. The central point of the ferromagnetic layer acts as a symmetry center, enabling the consideration of spatial symmetry of the Usadel function in the ferromagnetic layer to classify the form of solutions from the diffusion equation consistently with the phase state of the electron pair wave function. The critical temperature is calculated using self-consistent equations based on the superconducting order parameter. This method assumes that the electron pair wave function oscillates at a specific frequency. The reduction in critical temperature arises from the influence of pairing destroyers, acting as the eigenvalues of boundary conditions for the problem. These are roots obtained from the Usadel equation linkage between the superconductor and ferromagnet through boundary conditions at the interface. The π-phase state phenomenon within layered systems is analyzed by examining the variation of critical temperature with increasing thickness of the ferromagnetic layers.

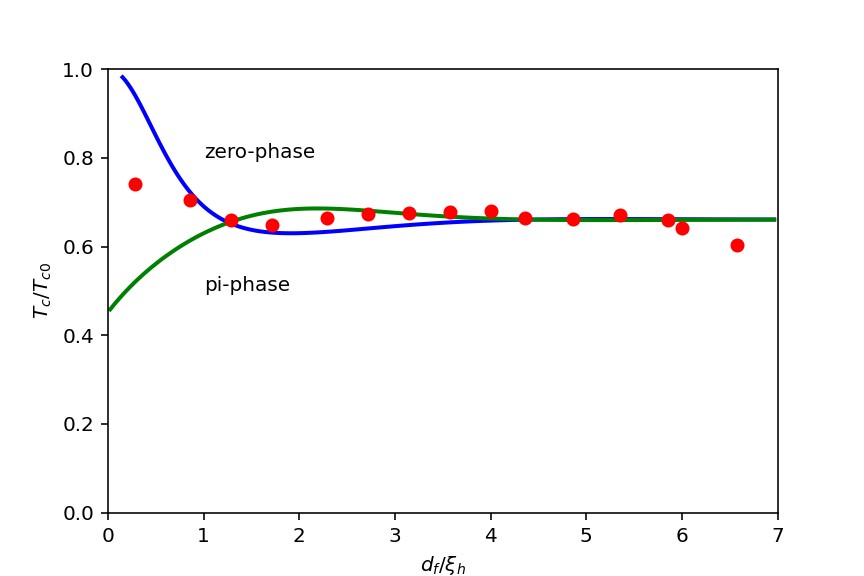
Main Results : The critical temperature equation describing the reduction of temperature in the superconducting state, expressed in terms of Cooper pairs destroyers, is related to the di-gamma function through a single-mode solution procedure. This procedure must be used together with the transcendental equation of Cooper pairs destroyers to find the minimum root, resulting in the highest critical temperature. Here, the phase state of the electron pair wave function determines the form of the boundary function which is a component of the transcendental equation, making numerical analysis necessary. However, when the thickness of the superconductor is less than the diffusion length, the transcendental equation provides an analytical root and the critical temperature has a simple analytical formula. In the special case where there is no resistance at the interface between the superconductor and the ferromagnet, the formula for the reduction of the critical temperature near the isolated critical temperature shows the existence of the π phase state. Numerical analysis of the critical temperature equation in the general case, with any thickness of the superconducting layer, confirms the existence of the π phase state. Comparing experimental results with theory, when the interfacial resistance condition is limited, reveals that the π phase state truly exists in a trilayer system of Niobium-Gadolinium-Niobium. This study also predicts the switching phenomenon of the superconducting state.

Conclusions  : (1) the single-mode solution is sufficient to analyze the experimental results of Nb/Gd/Nb trilayer structures (2) the interface boundary resistance is an important ingredient for the occurrence of the π phase state (3) the zero-and π- phase are the energetic favorable superconducting state in proximity effect (4) the transition of the superconducting phase between the zero-and π-phase can occur as the ferromagnetic thickness increases and (5) the re-entrance behavior of superconductivity is a distinctive characteristic of the zero-phase.