Necessary and Sufficient Conditions for the Concurrent Point of Cevians with Area-Bisecting and Perimeter-Bisecting Properties in a Given Triangle

Abstract

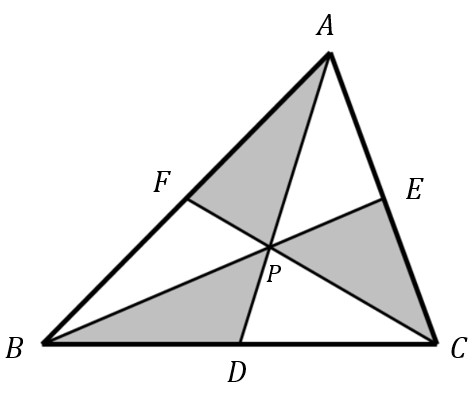
Background and Objectives : The problem of fairly dividing a pizza between two individuals such that both receive equal quantities has been a long-standing topic of mathematical interest. This has led to a range of studies involving various geometric shapes and principles to ensure equal division not only in terms of area but also in terms of boundary length (or crust). In 1994, Carter and Wagon demonstrated that a circular pizza could be equally divided into eight slices using four straight lines intersecting at any point, such that each of the resulting eight angles measures 45 degrees. This slicing method ensured each person received equal portions when slices were alternately distributed. Later in 2015, Nicollier extended this idea to equilateral triangular pizzas, introducing a division using six lines—three connecting an arbitrary interior point to the triangle’s vertices, and three drawn perpendicularly from that point to each side. By distributing these sections alternately, both individuals received equal areas and crust lengths. Further developments by Embacher and Humenberger in 2019 explored the division of acute or non-equilateral triangles into six smaller triangles from a chosen internal point. Their findings revealed that the area is equally divided when alternating regions are shaded black and white, but only if the point lies on the Stammler hyperbola—an important geometric curve containing the incenter, circumcenter, and excenter of the triangle. In 2020, Humenberger focused on unequal-sided triangular pizzas and proposed that crust bisection is guaranteed when the dividing point lies on a line connecting the incenter and circumcenter. For achieving area bisection, however, he utilized Cevians—line segments from each vertex to the opposite side intersecting at a common internal point—finding that equality in area occurs only if the intersection point lies along the triangle’s medians. Building upon this rich context, the current research aims to identify the necessary and sufficient conditions for a point within a triangle such that the Cevians intersecting at that point divide both the area and the perimeter of the triangle equally. While prior studies examined these two properties individually, this study focuses on their concurrent realization using only Cevians, which introduces a unique constraint that deepens the geometric inquiry.

Methodology : The investigation began with a conjecture formed through dynamic geometry software (GSP), which allowed for visual experimentation and hypothesis testing. Once a conjecture was formed, the authors pursued a rigorous mathematical proof using classical geometric theorems—chiefly, Ceva’s Theorem, which provides conditions for concurrency of Cevians in a triangle.

Key definitions were employed for precision:

• A Cevian is a line segment drawn from a vertex of a triangle to the opposite side.
• A median is a Cevian that intersects the opposite side at its midpoint.
• The main median refers to the median corresponding to the triangle’s axis of symmetry in an isosceles triangle.
• A point of Cevian concurrency is called a concurrent point.
• A centroid is the common point of intersection of all three medians of a triangle.

Main Results : This research focuses on investigating the geometric conditions associated with the concurrency point of Cevians in a given triangle that simultaneously induces two notable properties: first, that the concurrency point partitions the triangle into six smaller subregions of equal geometric relevance; and second, that this point serves as both an area-bisecting and a perimeter-bisecting point of the triangle. The findings of the study lead to the identification of a fundamental geometric characterization. The necessary and sufficient condition for the concurrency point of the Cevians to possess both the area-bisecting and the perimeter-bisecting properties can be precisely formulated as follows: in the case of an isosceles triangle, the concurrency point must lie on the main median, whereas in the case of a scalene triangle, the concurrency point must coincide with the centroid of the triangle. These conclusions establish a clear distinction between symmetric and asymmetric triangular configurations and highlight the unique and significant role of the centroid in a scalene triangle. The validity of these results has been rigorously established through proofs constructed by employing Ceva’s theorem, in conjunction with proportional reasoning concerning both triangular areas and the segment lengths determined by the Cevians. This methodological framework not only ensures the logical soundness of the arguments but also demonstrates the deep interrelationship between classical Ceva-type concurrency conditions and the division properties of both the area and the perimeter of triangles. The outcomes of this investigation contribute to the broader understanding of triangle geometry by providing a comprehensive condition that unifies two fundamental partitioning properties within a single concurrency framework.

Conclusions : The study offers a nuanced extension to prior works (Humenberger, 2020) by merging two types of fairness criteria (area and boundary) under a single geometric constraint—the concurrency of Cevians. In summary, the research contributes a precise characterization of geometric conditions under which a triangle can be equally divided—both in area and crust—via intersecting Cevians. The central conclusion is that:

• For isosceles triangles, the point of concurrency must lie on the main median.
• For scalene triangles, the point must be the centroid.

This result advances our understanding of fair division in geometric terms, with potential applications not only in recreational mathematics (e.g., pizza problems) but also in educational settings where concepts like medians, centroids, and Cevians are introduced.