เงื่อนไขจำเป็นและเพียงพอของจุดจวบของเส้นเชเวียนที่มีสมบัติ แบ่งครึ่งพื้นที่และเส้นรอบรูปของรูปสามเหลี่ยมที่กำหนด
คำสำคัญ:
แบ่งครึ่งพื้นที่ , เชเวียน , จุดจวบ , แบ่งครึ่งขอบ , การแบ่งอย่างยุติธรรมบทคัดย่อ
วัตถุประสงค์และที่มา : ปัญหาในการแบ่งพิซซาให้บุคคลสองคนได้รับปริมาณที่เท่ากันอย่างยุติธรรมเป็นหัวข้อที่นักคณิตศาสตร์ให้ความสนใจมาอย่างยาวนาน นำไปสู่การศึกษาหลากหลายที่เกี่ยวข้องกับรูปร่างเรขาคณิตต่าง ๆ และหลักการทางเรขาคณิต เพื่อให้เกิดการแบ่งที่เท่าเทียมกันไม่เพียงแต่ในด้านพื้นที่ แต่ยังรวมถึงความยาวของขอบ (หรือ crust) ด้วย ในปี ค.ศ. 1994 Carter และ Wagon ได้แสดงให้เห็นว่าพิซซารูปวงกลมสามารถแบ่งออกเป็น 8 ชิ้นเท่า ๆ กันโดยใช้เส้นตรง 4 เส้น ที่ตัดกัน ณ จุดใด ๆ โดยมุมที่เกิดขึ้นทั้ง 8 มุมมีขนาด 45 องศา ผลลัพธ์คือ หากแจกพิซซาที่ได้แบบสลับชิ้นกันระหว่างสองคน จะทำให้แต่ละคนได้รับปริมาณที่เท่ากันพอดี ต่อมาในปี ค.ศ. 2015 Nicollier ได้ขยายแนวคิดนี้ไปยังพิซซารูปสามเหลี่ยมด้านเท่า โดยใช้เส้นแบ่ง 6 เส้น ซึ่งประกอบด้วย 3 เส้นที่ลากจากจุดภายในใด ๆ ไปยังจุดยอดของรูปสามเหลี่ยม และอีก 3 เส้นที่ลากจากจุดเดียวกันไปตั้งฉากกับด้านของรูปสามเหลี่ยม จากนั้นแบ่งพิซซาที่ได้แบบสลับกัน ทำให้แต่ละคนได้รับทั้งพื้นที่และความยาวขอบที่เท่ากัน ในปี ค.ศ. 2019 Embacher และ Humenberger ได้ศึกษาการแบ่งรูปสามเหลี่ยม มุมแหลมหรือสามเหลี่ยมด้านไม่เท่า โดยใช้จุดภายในรูปสามเหลี่ยมเป็นจุดเริ่มต้นในการลากเส้น แบ่งรูปสามเหลี่ยมออกเป็นรูปสามเหลี่ยมย่อย 6 รูป สลับการระบายสีขาว-ดำ และพบว่า ผลรวมของพื้นที่ของรูปสามเหลี่ยมสีขาวจะเท่ากับผลรวมของพื้นที่ของรูปสามเหลี่ยมสีดำ ก็ต่อเมื่อ จุดภายในนั้นอยู่บนเส้นโค้งที่เรียกว่า Stammler hyperbola ซึ่งเป็นเส้นโค้งที่ผ่านจุดศูนย์กลางของวงกลมแนบใน (incenter) วงกลมล้อม (circumcenter) และวงกลมนอก (excenter) ของรูปสามเหลี่ยม ต่อมาในปี ค.ศ. 2020 Humenberger ได้เน้นการศึกษาสำหรับรูปสามเหลี่ยมด้านไม่เท่า โดยเสนอว่าการแบ่งครึ่งขอบจะเกิดขึ้นได้ ถ้าจุดแบ่งอยู่บนเส้นตรงที่เชื่อมระหว่างจุดศูนย์กลางของวงกลมแนบในและวงกลมล้อม ส่วนการแบ่งครึ่งพื้นที่ให้เท่ากันนั้นต้องใช้แนวคิดของ เส้นเชเวียน (Cevian) ซึ่งเป็นเส้นตรงที่ลากจากจุดยอดของรูปสามเหลี่ยมไปยังด้านตรงข้ามโดยตัดกันที่จุดภายในจุดเดียวกัน และพบว่าการแบ่งครึ่งพื้นที่อย่างเท่าเทียมจะเกิดขึ้นได้ ก็ต่อเมื่อ จุดตัดอยู่บนเส้นมัธยฐานของรูปสามเหลี่ยม จากพื้นฐานดังกล่าว งานวิจัยนี้มีวัตถุประสงค์เพื่อหา เงื่อนไขจำเป็นและเพียงพอของจุดภายในรูปสามเหลี่ยมที่ทำให้เส้นเชเวียนทั้งสามจวบกัน ณ จุดนั้น สามารถแบ่งทั้งพื้นที่และเส้นรอบรูปของรูปสามเหลี่ยมได้อย่างเท่าเทียมกัน โดยเน้นเฉพาะการใช้เส้นเชเวียนเท่านั้น ซึ่งเป็นข้อจำกัดทางเรขาคณิตที่เพิ่มความลึกในการวิเคราะห์
วิธีดำเนินการวิจัย : ผู้วิจัยเริ่มจากการตั้งข้อสันนิษฐานผ่านโปรแกรมเรขาคณิตพลวัต (GSP) ซึ่งช่วยให้สามารถสำรวจทางภาพและตรวจสอบสมมติฐานได้อย่างยืดหยุ่น จากนั้นจึงเข้าสู่กระบวนการพิสูจน์เชิงคณิตศาสตร์อย่างเคร่งครัด โดยใช้ทฤษฎีบทเชวา (Ceva’s Theorem) เป็นหลัก ซึ่งใช้เพื่อพิสูจน์เงื่อนไขของการจวบกันของเส้นเชเวียนภายในรูปสามเหลี่ยม
นิยามสำคัญที่ใช้ในงานวิจัย ได้แก่ :
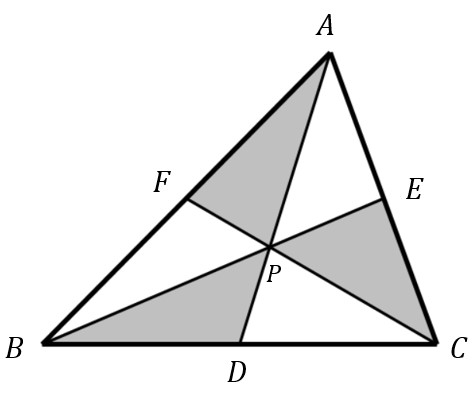
- เส้นเชเวียน (Cevian) คือเส้นตรงที่ลากจากจุดยอดไปยังด้านตรงข้ามของรูปสามเหลี่ยม
- เส้นมัธยฐาน (Median) คือเส้นเชเวียนที่ตัดด้านตรงข้าม ณ จุดกึ่งกลาง
- เส้นมัธยฐานหลัก (Main Median) คือเส้นมัธยฐานที่อยู่บนแกนสมมาตรของสามเหลี่ยมหน้าจั่ว
- จุดจวบของเส้นเชเวียน (Concurrent Point) คือจุดที่เส้นเชเวียนทั้งสามตัดกัน
- จุดเซนทรอยด์ (Centroid) คือจุดตัดของมัธยฐานทั้งสาม
ผลการวิจัย : งานวิจัยนี้มุ่งศึกษาถึงเงื่อนไขทางเรขาคณิตที่เกี่ยวข้องกับจุดจวบของเส้นเชเวียนในรูปสามเหลี่ยมที่กำหนดที่ทำให้จุดดังกล่าวมีสมบัติสำคัญสองประการ ได้แก่ (1) การทำให้รูปสามเหลี่ยมถูกแบ่งออกเป็น 6 ส่วนย่อยที่มีความสำคัญ ทางเรขาคณิต และ (2) การทำหน้าที่เป็นจุดที่สามารถแบ่งครึ่งทั้งพื้นที่และเส้นรอบรูปของรูปสามเหลี่ยมได้ในเวลาเดียวกัน ผลการวิจัยนำไปสู่การระบุเงื่อนไขทางเรขาคณิตที่มีความสำคัญพื้นฐาน โดยสามารถสรุปเป็นทฤษฎีบทได้ว่า เงื่อนไขจำเป็นและเพียงพอของจุดจวบของเส้นเชเวียนที่จะทำให้เกิดสมบัติการแบ่งครึ่งทั้งพื้นที่และเส้นรอบรูปนั้น มีลักษณะดังนี้: สำหรับรูปสามเหลี่ยมหน้าจั่ว จุดจวบต้องอยู่บนเส้นมัธยฐานหลัก ขณะที่สำหรับรูปสามเหลี่ยมด้านไม่เท่า จุดจวบดังกล่าวจะต้องเป็นจุดเซนทรอยด์ของรูปสามเหลี่ยมเท่านั้น ผลลัพธ์นี้แสดงให้เห็นถึงความแตกต่างระหว่างสามเหลี่ยมที่มีความสมมาตร (isosceles) และสามเหลี่ยมที่ไม่สมมาตร (scalene) รวมถึงชี้ให้เห็นถึงบทบาทสำคัญของจุดเซนทรอยด์ที่มีเอกลักษณ์เฉพาะสำหรับสามเหลี่ยมด้านไม่เท่า ความถูกต้องของผลลัพธ์เหล่านี้ได้รับการพิสูจน์อย่างเป็นระบบ โดยอาศัยการประยุกต์ใช้ทฤษฎีบทเชวา (Ceva’s theorem) ร่วมกับการให้เหตุผลเชิงสัดส่วนทั้งในด้านของพื้นที่ย่อยภายในรูปสามเหลี่ยมและความยาวของส่วนของเส้นตรงที่เกิดจากการแบ่งโดยเส้นเชเวียน กรอบวิธีการดังกล่าวไม่เพียงแต่สร้างความมั่นใจในความถูกต้องของข้อพิสูจน์ แต่ยังสะท้อนให้เห็นถึงความสัมพันธ์ระหว่างเงื่อนไขการเกิดจุดจวบแบบเชวา (Ceva-type concurrency) กับสมบัติการแบ่งครึ่งพื้นที่และเส้นรอบรูปของรูปสามเหลี่ยม ผลการวิจัยครั้งนี้จึงถือเป็นการเพิ่มพูนความเข้าใจเกี่ยวกับเรขาคณิตของสามเหลี่ยม โดยนำเสนอเงื่อนไขเชิงบูรณาการที่เชื่อมโยงสมบัติการแบ่งสองประการไว้ภายใต้กรอบแนวคิดของจุดจวบเพียงจุดเดียว
สรุปผลการวิจัย : งานวิจัยนี้เป็นการต่อยอดจากงานที่ผ่านมา (Humenberger, 2020) โดยรวมเกณฑ์ความเท่าเทียมกันทั้งในด้านของพื้นที่และเส้นรอบรูปให้อยู่ภายใต้ข้อจำกัดทางเรขาคณิตเดียวกัน กล่าวคือการจวบกันของเส้นเชเวียน โดยพบว่า เงื่อนไขทางเรขาคณิตที่แม่นยำสำหรับจุดภายในรูปสามเหลี่ยมที่สามารถแบ่งพื้นที่และเส้นรอบรูปได้อย่างเท่าเทียมโดยใช้เส้นเชเวียนเท่านั้น สรุปได้ดังนี้ :
- สำหรับสามเหลี่ยมหน้าจั่ว: จุดจวบต้องอยู่บนเส้นมัธยฐานหลัก
- สำหรับสามเหลี่ยมด้านไม่เท่า: จุดจวบต้องเป็นจุดเซนทรอยด์
ผลลัพธ์นี้ช่วยเพิ่มพูนความเข้าใจด้านการแบ่งอย่างเท่าเทียมในทางเรขาคณิต และสามารถนำไปใช้ในการศึกษาคณิตศาสตร์เพื่อเสริมสร้างแนวคิดเรื่องมัธยฐาน จุดศูนย์กลาง และโครงสร้างสามเหลี่ยมได้อย่างมีประสิทธิภาพ
เอกสารอ้างอิง
Carter, L., & Wagon, S. (1994). Proof without words: fair allocation of a pizza. Mathematics Magazine, 67(4), 267.
Embacher, F., & Humenberger, H. (2019). A note on the Stammler hyperbola. The American Mathematical Monthly, 126(9), 841–844.
Humenberger, H. (2020). Fair sharing of triangular pizzas. Mathematics Magazine, 93(3), 64-174.
Nicollier, G. (2015). Proof without words: half issues in the equilateral triangle and fair pizza sharing. Mathematics Magazine, 88(5), 337.
Posamentier, A. S. (1984). Excursion in advanced euclidean geometry. (Revised edition). USA: Addison-Wesley Publishing Company, Inc.
ดาวน์โหลด
เผยแพร่แล้ว
รูปแบบการอ้างอิง
ฉบับ
ประเภทบทความ
สัญญาอนุญาต
ลิขสิทธิ์ (c) 2025 คณะวิทยาศาสตร์ มหาวิทยาลัยบูรพา

อนุญาตภายใต้เงื่อนไข Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Burapha Science Journal is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) licence, unless otherwise stated. Please read our Policies page for more information



