Performance Comparison of the Linear Regression Model Based on Nonparametric Bootstrap Methods

Abstract

Background and Objectives : Regression analysis is a widely used statistical method for predicting or forecasting the value of a dependent variable from given values of independent variables. Linear regression analysis has several underlying assumptions about errors, but in some situations, the data may not meet these assumptions, leading to prediction errors. To address this issue, researchers have developed nonparametric regression models that do not rely on assumptions about the distribution of errors, providing greater flexibility. The objective of this research was to investigate and compare the performance of linear regression models under nonparametric bootstrap methods. This research utilized two different nonparametric bootstrap methods; the percentile bootstrap method (also known as the bootstrap-p method) and the studentized bootstrap method (or bootstrap-t method). The bootstrap-p method is widely accepted due to its simple resampling technique, which involves repeatedly sampling with replacement to create multiple bootstrap samples and then calculating the distribution of the estimator. This method is particularly useful when the sample size is small, and the data distribution is unknown. In contrast, the bootstrap-t method enhances the bootstrap-p method by incorporating the concept of studentization. This involves adjusting the bootstrap samples according to the standard error of the estimator, resulting in more accurate confidence intervals and reduced bias.

Methodology : The performance of the bootstrap regression models was examined using Monte Carlo simulation, based on the distribution of error terms ( ) with three types of skew-normal distributions; left-skewed, right-skewed, and symmetric, which are commonly observed in real data. The parameters of skew-normal distribution include a location parameter(), a scale parameter (² ) , and a shape parameter ( ). These parameters for data simulation were selected to reflect different levels of skewness and variance, ensuring a comprehensive evaluation of the performance of bootstrap regression analysis across the three distribution types. The parameters were set as follows:=0 ,² =1,2,5,10 , and   =-1,0,1, i.e., SN(0, ², ) . For the independent variable, data was simulated under normal distribution with parameters _x=3 and ²_x=2.25  i.e., X   N(3,2.25). Sample sizes of 20, 30, 50, and 100 were used. Confidence intervals for regression coefficients and regression models were constructed using both bootstrap methods at a 95% confidence level, with 1,000 repetitions for each situation. The performance of the regression coefficient estimates was compared using the coefficient mean, the standard deviation of the regression coefficient, and the root mean squared error of the regression coefficient were presented as the criteria of point estimation. Also, the performance of interval estimation was compared with coverage probability, average width, and standard deviation of interval width. Additionally, both bootstrap regression models were applied to two real datasets: newborn birth weights and grade point averages, comparing the performance of the best regression models based on the coefficient of determination, Akaike’s information criterion, Bayesian information criterion, and mean squared error.

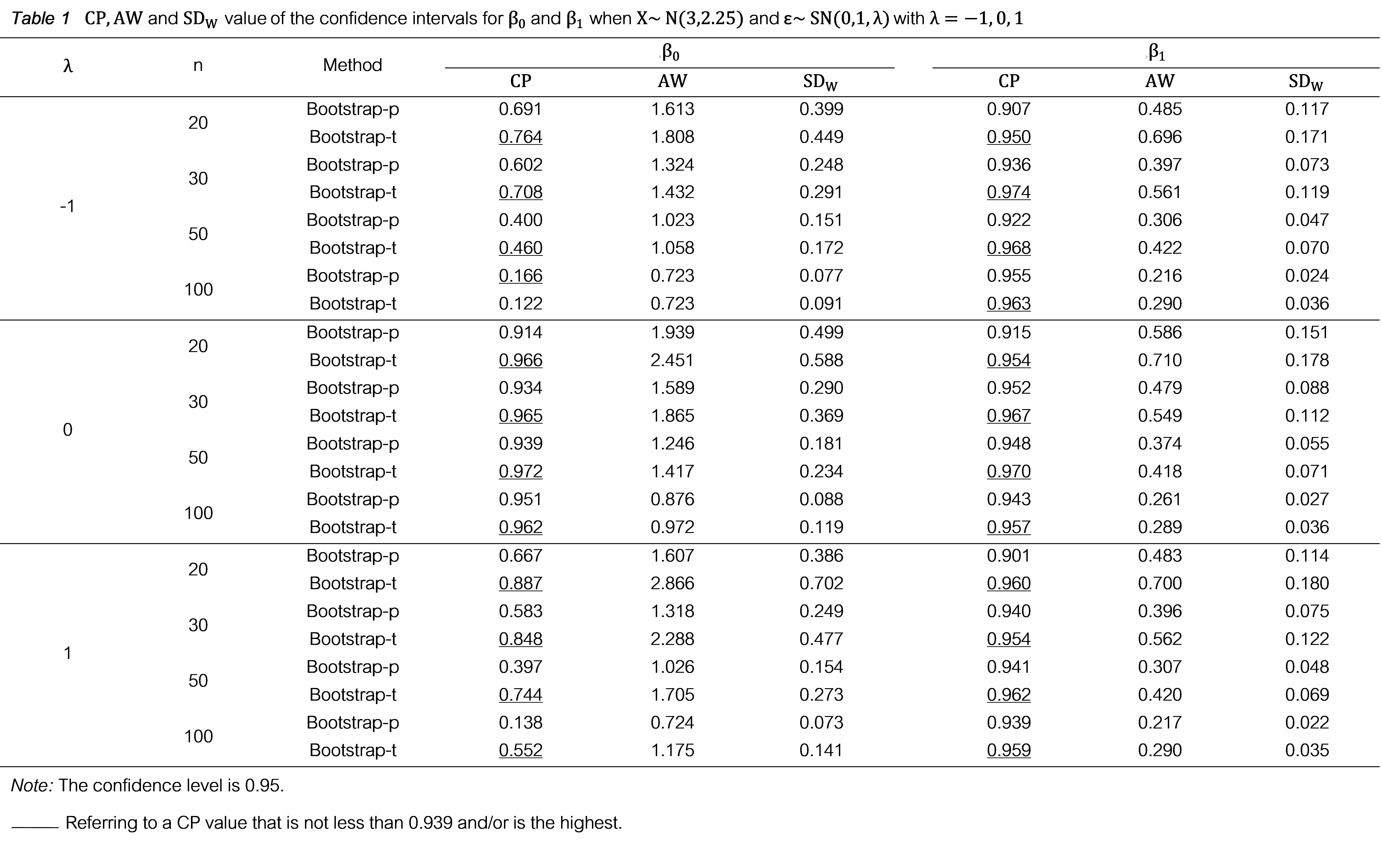
Main Results : The simulation study aimed at comparing the efficiency of confidence intervals for regression coefficients found that, as the sample size increases, the overall coverage probability increases, except in cases where the error distribution was skewed for the intercept parameter. Additionally, the average width of the interval, and the standard deviation of the interval width tend to decrease in all parameter sets. In most cases, the bootstrap-t method consistently achieved the highest coverage probability. The comparison of the performance of bootstrap regression models in parameter estimation indicated that, for all sample sizes, the mean regression coefficient, which is the bootstrap estimate of the regression coefficient, closely approximated the parameter values. Additionally, as the sample size increased, the standard deviation of the regression coefficient and the root mean squared error of the regression coefficient decreased in all cases. This implies that the efficiency of the regression models improves with larger sample sizes. Furthermore, for all sample sizes, the bootstrap-t regression models provided a lower root mean squared error of the regression coefficient compared to the bootstrap-p regression models, indicating better performance. However, in cases where the random error terms followed a symmetric distribution and the sample size was small, the bootstrap-p method demonstrated higher efficiency in estimating the regression coefficients.

Conclusions : The comparison of bootstrap regression models revealed that both methods provided estimates close to the true parameters, indicating their effectiveness in handling different error distributions. However, the bootstrap-t method consistently demonstrated superior performance, particularly in terms of the coverage probability and the root mean squared error, which are key measures of accuracy in estimating regression coefficients. This suggests that the bootstrap-t method is more reliable, making it a more credible choice for constructing confidence intervals and estimating regression coefficients. As the sample size increased, the accuracy and reliability of the bootstrap methods improved, resulting in narrower confidence intervals and more precise regression coefficient estimates. Additionally, the results obtained from applying the bootstrap methods to real data were consistent with the simulations study under skew-normal distributions. Therefore, bootstrap methods are alternative methods for estimating confidence intervals and regression coefficients. They enhance the predictive efficiency of regression models, especially when parametric assumptions are violated. This study is significant and beneficial for both researchers and practitioners. It emphasizes the thorough consideration of sample size and error distribution to select the appropriate regression method.