การเปรียบเทียบประสิทธิภาพตัวแบบการถดถอยเชิงเส้น ภายใต้วิธีบูตสแทร็ปแบบไม่อิงพารามิเตอร์

บทคัดย่อ

วัตถุประสงค์และที่มา : การวิเคราะห์การถดถอยเป็นวิธีการทางสถิติที่ใช้กันอย่างแพร่หลายในการทำนายหรือพยากรณ์ค่าของตัวแปรตามจากค่าที่กำหนดให้ของตัวแปรอิสระ โดยการวิเคราะห์การถดถอยเชิงเส้นนั้นมีข้อสมมติเบื้องต้นเกี่ยวกับความคลาดเคลื่อนหลายประการ ซึ่งในบางสถานการณ์ข้อมูลที่นำมาใช้อาจไม่เป็นไปตามข้อสมมติเบื้องต้นทำให้เกิดความคลาดเคลื่อนหรือความผิดพลาดในการพยากรณ์ได้ เพื่อแก้ปัญหาดังกล่าว นักวิจัยจึงได้พัฒนาตัวแบบการถดถอยแบบไม่อิงพารามิเตอร์ขึ้นมา ซึ่งไม่ต้องคำนึงถึงข้อสมมติเบื้องต้นดังกล่าว ทำให้มีความยืดหยุ่นมากขึ้น การศึกษาครั้งนี้มีวัตถุประสงค์เพื่อศึกษาและเปรียบเทียบประสิทธิภาพของตัวแบบการถดถอยเชิงเส้นภายใต้วิธีบูตสแทร็ปแบบไม่อิงพารามิเตอร์ 2 วิธี ได้แก่ วิธีบูตสแทร็ปแบบเปอร์เซ็นไทล์ หรือที่รู้จักกันในชื่อวิธีบูตสแทร็ปพี และวิธีบูตสแทร็ปแบบสติวเดนต์หรือวิธีบูตสแทร็ปที ซึ่งวิธีบูตสแทร็ปพีเป็นเทคนิคที่ได้รับการยอมรับอย่างกว้างขวางเนื่องจากมีรูปแบบของการสุ่มข้อมูลที่ไม่ซับซ้อน โดยการสุ่มตัวอย่างข้อมูลซ้ำด้วยการแทนที่คืนเพื่อสร้างตัวอย่างบูตสแทร็ปหลาย ๆ ตัวอย่าง จากนั้นทำการคำนวณการแจกแจงของตัวประมาณ วิธีนี้มีประโยชน์อย่างยิ่งเมื่อตัวอย่างมีขนาดเล็กและการแจกแจงของข้อมูลไม่เป็นที่รู้จัก ในทางกลับกัน วิธีบูตสแทร็ปที เป็นการปรับปรุงวิธีบูตสแทร็ปพีโดยการนำแนวคิดของการสติวเดนท์มาใช้ซึ่งเกี่ยวข้องกับการปรับตัวอย่างบูตสแทร็ปตามค่าความคลาดเคลื่อนมาตรฐานของตัวประมาณ ทำให้ได้ช่วงความเชื่อมั่นที่แม่นยำมากขึ้นและลดความเอนเอียง

วิธีดำเนินการวิจัย : งานวิจัยนี้ทำการจำลองข้อมูลด้วยเทคนิคมอนติคาร์โลภายใต้ค่าความคลาดเคลื่อน ( )มีการแจกแจงเบ้ปรกติ (Skew-Normal Distributions : SN) 3 ลักษณะ คือ เบ้ซ้าย เบ้ขวา และสมมาตร ซึ่งเป็นการแจกแจงที่พบได้บ่อยในข้อมูลจริง โดยมีพารามิเตอร์ 3 ตัว ได้แก่ พารามิเตอร์บ่งตำแหน่ง (Location Parameter : ) พารามิเตอร์บ่งขนาด (Scale Parameter : ² ) และพารามิเตอร์บ่งรูปร่าง (Shape Parameter : ) โดยพารามิเตอร์สำหรับการจำลองข้อมูลถูกเลือกเพื่อสะท้อนถึงระดับความเบ้และความแปรปรวนที่แตกต่างกัน ทำให้การประเมินประสิทธิภาพในการวิเคราะห์การถดถอยภายใต้วิธีบูตสแทร็ปมีความครอบคลุมกับลักษณะการแจกแจงทั้งสามรูปแบบ กำหนดให้ =0 , ² =1,2,5,10 และ  =-1,0,1  นั่นคือ  SN(0, ², )และจำลองข้อมูลสำหรับตัวแปรอิสระภายใต้การแจกแจงปรกติ โดยมีพารามิเตอร์ 2 ตัว ได้แก่ ค่าเฉลี่ย (_x) และค่าความแปรปรวน (²_x) กำหนดให้ _x=3 และ²_x=2.25   นั่นคือ  X   N(3,2.25)  ขนาดตัวอย่างที่ใช้ในจำลอง คือ 20, 30, 50 และ 100 ทำการสร้างช่วงความเชื่อมั่นของสัมประสิทธิ์การถดถอยและสมการถดถอยด้วยวิธีบูตสแทร็ปทั้งสองวิธี ที่ระดับความเชื่อมั่น 95% โดยกระทำซ้ำ 1,000 รอบในแต่ละสถานการณ์ จากนั้นทำการเปรียบเทียบประสิทธิภาพในการประมาณค่าสัมประสิทธิ์การถดถอย โดยใช้ค่าสัมประสิทธิ์การถดถอยเฉลี่ย ค่าส่วนเบี่ยงเบนมาตรฐานของสัมประสิทธิ์การถดถอย และค่ารากที่สองของคลาดเคลื่อนกำลังสองเฉลี่ยของสัมประสิทธิ์การถดถอย เป็นค่าเกณฑ์ในการเปรียบเทียบตัวประมาณแบบจุด และประสิทธิภาพของตัวประมาณแบบช่วงถูกเปรียบเทียบโดยใช้ค่าความน่าจะเป็นคุ้มรวม ค่าความกว้างเฉลี่ยของช่วง และค่าส่วนเบี่ยงเบนมาตรฐานของความกว้างของช่วง อีกทั้ง การศึกษาครั้งนี้ได้ประยุกต์ใช้ตัวแบบการถดถอยบูตสแทร็ปทั้งสองวิธีกับข้อมูลจริง 2 ชุด ได้แก่ ชุดข้อมูลน้ำหนักทารกแรกเกิด และชุดข้อมูลเกรดเฉลี่ย โดยเปรียบเทียบประสิทธิภาพของสมการถดถอยที่ดีที่สุดจากเกณฑ์ค่าสัมประสิทธิ์การกำหนด เกณฑ์สารสนเทศของอะกะอิเกะ เกณฑ์สารสนเทศของเบส์ และค่าคลาดเคลื่อนกำลังสองเฉลี่ย

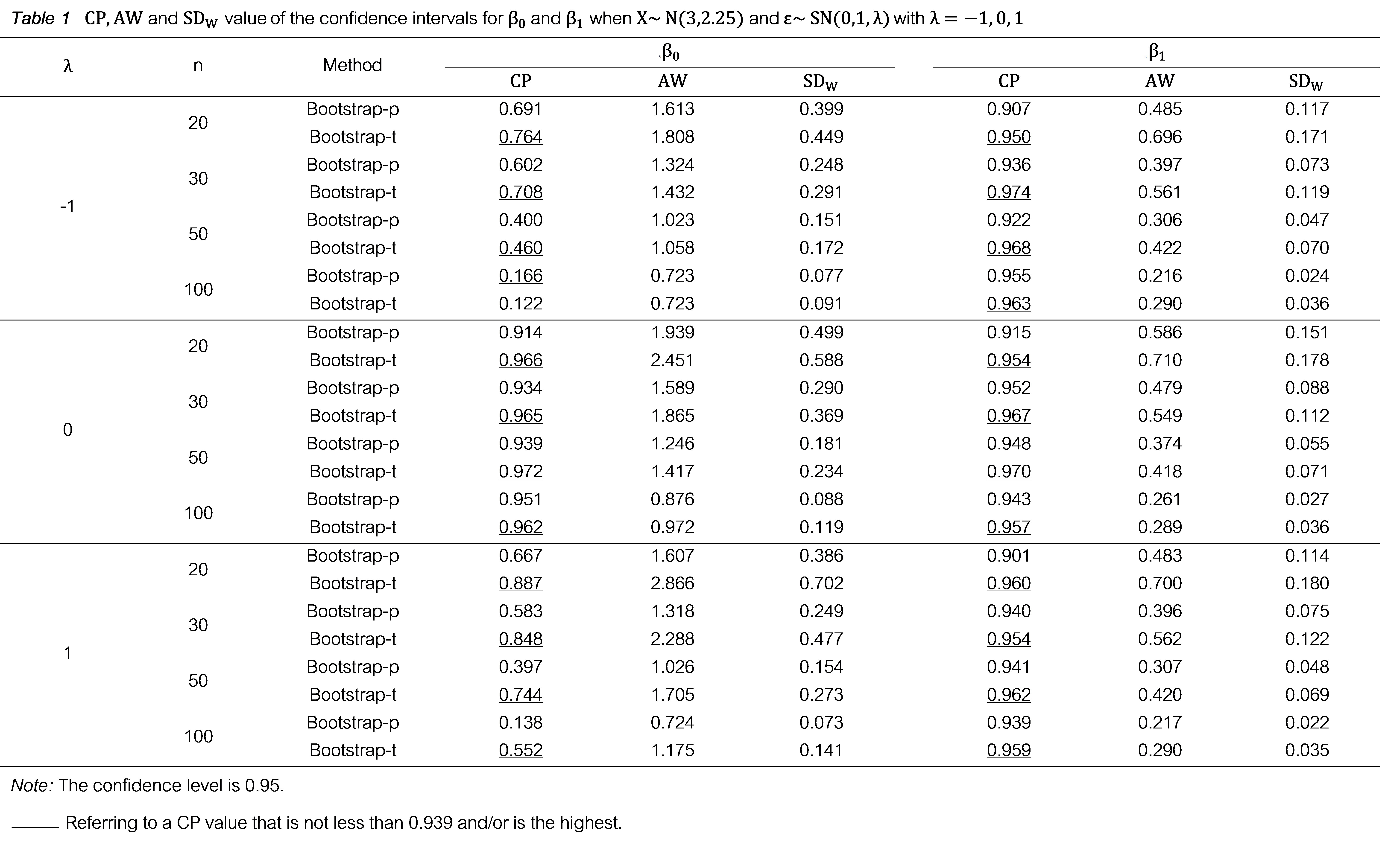
ผลการวิจัย : จากการศึกษาจำลองข้อมูลเชิงสถิติเพื่อเปรียบเทียบประสิทธิภาพของช่วงความเชื่อมั่นสำหรับสัมประสิทธิ์การถดถอย พบว่าเมื่อขนาดตัวอย่างเพิ่มขึ้นค่าความน่าจะเป็นคุ้มรวมมีค่าเพิ่มขึ้น ยกเว้นกรณีที่ค่าคลาดเคลื่อนมีการ  แจกแจงแบบเบ้สำหรับพารามิเตอร์ค่าคงที่ ค่าความกว้างเฉลี่ยของช่วง และค่าส่วนเบี่ยงเบนมาตรฐานของความกว้างของช่วงมีแนวโน้มลดลงในทุกเซตพารามิเตอร์ โดยส่วนมากวิธีบูตสแทร็ปทีมีค่าความน่าจะเป็นคุ้มรวมมากที่สุด และผลการเปรียบเทียบประสิทธิภาพของสมการถดถอยบูตสแทร็ปในการประมาณค่าพารามิเตอร์ พบว่าในทุกขนาดตัวอย่างค่าสัมประสิทธิ์การถดถอยเฉลี่ยซึ่งเป็นค่าประมาณสัมประสิทธิ์การถดถอยด้วยวิธีบูตสแทร็ปมีค่าใกล้เคียงค่าพารามิเตอร์ และเมื่อขนาดตัวอย่างเพิ่มขึ้นค่าส่วนเบี่ยงเบนมาตรฐานของสัมประสิทธิ์การถดถอย และค่ารากที่สองของค่าคลาดเคลื่อนกำลังสองเฉลี่ยลดลงในทุกกรณี นั่นคือสมการถดถอยจะมีประสิทธิภาพเพิ่มขึ้นเมื่อขนาดตัวอย่างเพิ่มขึ้น นอกจากนี้ในทุกขนาดตัวอย่างสมการถดถอยบูตสแทร็ปทีให้ค่ารากที่สองของค่าคลาดเคลื่อนกำลังสองเฉลี่ยน้อยกว่าสมการถดถอย  บูตสแทร็ปพี ซึ่งบ่งชี้ถึงประสิทธิภาพที่ดีกว่า ยกเว้นกรณีที่ค่าความคลาดเคลื่อนสุ่มมีการแจกแจงแบบสมมาตรและขนาดตัวอย่างเล็ก จะพบว่าวิธีบูตสแทร็ปพีมีประสิทธิภาพในการประมาณค่าสัมประสิทธิ์การถดถอยสูงกว่า

สรุปผลการวิจัย : การเปรียบเทียบสมการถดถอยบูตสแทร็ปเผยให้เห็นว่าวิธีทั้งสองให้ค่าประมาณที่ใกล้เคียงกับพารามิเตอร์จริง ซึ่งบ่งชี้ถึงประสิทธิภาพในการจัดการกับการแจกแจงความคลาดเคลื่อนที่แตกต่างกัน อย่างไรก็ตาม วิธีบูตสแทร็ปทีแสดงให้เห็นถึงประสิทธิภาพที่เหนือกว่าวิธีบูตสแทร็ปพีอย่างต่อเนื่อง โดยเฉพาะในแง่ของค่าความน่าจะเป็นคุ้มรวมและค่ารากที่สองของค่าคลาดเคลื่อนกำลังสองเฉลี่ย ซึ่งเป็นมาตรวัดสำคัญของความแม่นยำในการประมาณค่าสัมประสิทธิ์การถดถอย บ่งชี้ว่าวิธีบูตสแทร็ปทีมีความน่าเชื่อถือมากกว่า ทำให้เป็นทางเลือกที่น่าเชื่อถือในการสร้างช่วงความเชื่อมั่นและการประมาณค่าสัมประสิทธิ์การถดถอย และเมื่อขนาดตัวอย่างเพิ่มขึ้นความแม่นยำและความน่าเชื่อถือของวิธีบูตสแทร็ปจะดีขึ้น ทำให้ช่วงความเชื่อมั่นแคบลงและการประมาณค่าสัมประสิทธิ์การถดถอยแม่นยำมากขึ้น นอกจากนี้ ผลลัพธ์ที่ได้จากการประยุกต์ใช้กับข้อมูลจริงนั้นสอดคล้องกับการจำลองข้อมูลเชิงสถิติภายใต้การแจกแจงแบบเบ้ปรกติ ดังนั้น วิธีบูตสแทร็ปจึงเป็นวิธีทางเลือกในการประมาณค่าช่วงความเชื่อมั่นและการประมาณค่าสัมประสิทธิ์การถดถอยที่ทำให้สมการถดถอยที่ได้นั้นมีประสิทธิภาพในการพยากรณ์ โดยเฉพาะเมื่อข้อสมมติของวิธีอิงพารามิเตอร์ไม่เป็นจริง ผลการศึกษานี้มีความสำคัญและประโยชน์ต่อทั้งนักวิจัยและผู้ปฏิบัติงาน ซึ่งเน้นถึงการพิจารณาขนาดตัวอย่างและการแจกแจงความคลาดเคลื่อนอย่างรอบคอบเพื่อเลือกวิธีการถดถอยที่เหมาะสม